Answer:
The required probability is 0.6517
Explanation:
Consider the provided information.
North Catalina State University's students can be approximated by a normal model with mean 130 and standard deviation 8 points.
μ₁ = 130 and σ₁ = 8
Chapel Mountain University's students can be approximated by a normal model with mean 120 and standard deviation 10 points.
μ₂ = 120 and σ₂ = 10
As both schools have IQ scores which is normally distributed, distribution of this difference will also be normal with a mean of μ₁-μ₂ and standard deviation will be
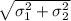
Therefore,
μ = 130-120=10
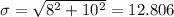
Now determine the probability of North Catalina State University student's IQ is at least 5 points higher than the Chapel Mountain University student's IQ:
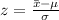
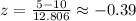
Now by using the z table we find the z- score of -0.39 is 0.6517.
Hence, the required probability is 0.6517