Answer:
It take 65 people to maximize the revenue.
Explanation:
Consider the provided information.
Let x is the number of people who take part in trip.
They charge $50 per person and they will reduce the price per person for all riders by $0.50 for each person excess of 30.
The price for each person is
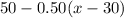 where x is greater or equal to 30.
where x is greater or equal to 30.
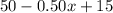
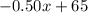
Now write a revenue function by multiplying the number of people with the price per person.
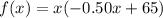
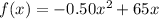
We need to maximize the company's revenue.
The above function is a parabola that opens downward because the coefficient of x²is negative.
Therefore, the maximum of the function is at its vertex.
If the equation of the parabola is
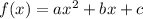 then we can find the coordinate of vertex at
then we can find the coordinate of vertex at
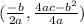
Calculate the value of
 for the function
for the function
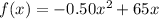 .
.
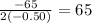
Therefore, it take 65 people to maximize the revenue.