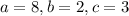Question

Mr. Casey writes the equation 40 = 16 + 24 = a(b + c). What whole

numbers can he choose for a, b, and cif he wants b and c to have no
common factors greater than 1?

Answer 1

`a=8,b=2,c=3`

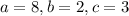
Explanation:

Given:

`40=16+24=a(b+c)`

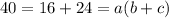
Now, in order to write 16 + 24 into a product of two numbers, we need to find the factors of 16 and 24.

Factors of 16 = 1, 2, 4, 8, 16.

Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24.

Now, common factors for 16 and 24 are 1, 2, 4 and 8.

Now, the values of
`b\textrm{ and }c` should be such that there should be no common factors between them except 1. In other words,
`b\textrm{ and }c` are prime numbers.

So, in order to get prime numbers for
`b\textrm{ and }c`, we should take the greatest common factor for 16 and 24 which is 8.

Therefore 40 = 16 + 24 can rewritten as:

`16+24=8(2+3)`

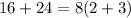
So,
`a=8,b=2,c=3`