Answer:

Explanation:
Unlike quadratic equations, cubic equations might be harder to solve. Therefore, one useful approach is to group and factor terms:
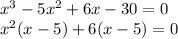
the term (x-5) now appears on both parts of the equation and can be factored as follows:
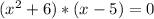
From here, we can find all three roots to the function:
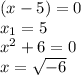
The only real root is 5 since there are no real square roots for negative numbers, the complex roots are:
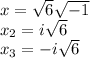
The zeroes of the polynomial funtion are:
