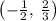Answer:
The answer in interval notation is
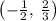
Explanation:
Consider the provided inequality.
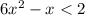
Subtract 2 from both sides.
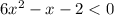



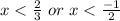
The value of function
 is positive for
is positive for
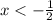
The value function
 is zero at
is zero at
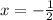
The value function
 is negative for
is negative for
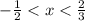
The value function
 is zero at
is zero at
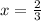
The value function
 is positive for
is positive for

Since we want the value of function less than 0, so the required interval which satisfy the condition < 0 is:
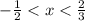
The required number line is shown below:
The answer in interval notation is