Question

0.0200 M Fe3+ is initially mixed with 1.00 M oxalate ion, C2O42-, and they react according to the equation: Fe3+(aq) + 3 C2O42-(aq) ⇄ [Fe(C2O4)3]3-(aq) Kc = 1.67 × 1020 What is the concentration of Fe3+(aq) when equilibrium is reached? 1.67 × 1020 M 8.35 × 10-19 M 6.9a × 1021 M 1.44 × 10-22 M 0.980 aM 0.940 M 0.0100 atm

Answer 1

Answer : The concentration of
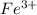`Fe^(3+)` at equilibrium is 0 M.

Solution : Given,

Concentration of
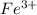`Fe^(3+)` = 0.0200 M

Concentration of
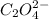`C_2O_4^(2-)` = 1.00 M

The given equilibrium reaction is,

`Fe^(3+)(aq)+3C_2O_4^(2-)(aq)\rightleftharpoons [Fe(C_2O_4)_3]^(3-)(aq)`

Initially conc. 0.02 1.00 0

At eqm. (0.02-x) (1.00-3x) x

The expression of
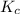`K_c` will be,

`K_c=([[Fe(C_2O_4)_3]^(3-)])/([C_2O_4^(2-)]^3[Fe^(3+)])`

`1.67* 10^(20)=((x)^2)/((1.00-3x)^3* (0.02-x))`

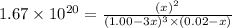
By solving the term, we get:

`x=0.02M`

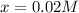
Concentration of
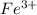`Fe^(3+)` at equilibrium = 0.02 - x = 0.02 - 0.02 = 0 M

Therefore, the concentration of
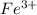`Fe^(3+)` at equilibrium is 0 M.