Answer:
(a)
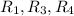
(b)
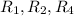
(c)
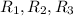
(d)

Explanation:
Since,
A relation R defined on A is called reflexive if,
∀ x ∈ A, (x, x)∈ R
It is called symmetric,
∀ x, y ∈ A, if (x, y)∈ R then (x, y)∈ R such that x ≠ y,
It is called anti symmetric,
∀ x, y ∈ A, if (x, y)∈ R then (x, y)∈ R such that x = y,
It is called transitive,
∀ x, y, z ∈ A, if (x, y)∈ R and (y, z)∈ R then (x, z)∈ R such that x ≠ y,
Given set,
{0, 1, 2, 3},
Also, the relation defined on the set are,
•
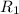 = {(0, 0),(1, 1),(2, 2),(3, 3)}
= {(0, 0),(1, 1),(2, 2),(3, 3)}
•
 = {(1, 1),(2, 2),(3, 3)}
= {(1, 1),(2, 2),(3, 3)}
•
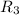 = {(0, 0),(1, 1),(2, 0),(2, 2),(2, 3),(3, 3)}
= {(0, 0),(1, 1),(2, 0),(2, 2),(2, 3),(3, 3)}
•
 = {(0, 0),(0, 1),(1, 0),(1, 1),(2, 2),(3, 3)}
= {(0, 0),(0, 1),(1, 0),(1, 1),(2, 2),(3, 3)}
Hence, by the above explanation it is clear that,
Relations which are reflexive,
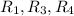
Relations which are symmetric,
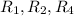
Relations which are anti-symmetric,
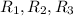
Relations which are transitive,
