Answer:
a) 70
b) 10π ft²/ft
c) 0.24 ft/sec
Explanation:
1) y = x³ + 2x
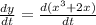
or
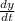 =
=
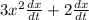
at
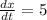 and x = 2
and x = 2
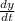 =
=
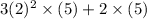
or
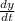 = 60 + 10 = 70
= 60 + 10 = 70
2) A = πr² ft²
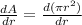
or
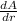 = 2(πr)
= 2(πr)
at r = 5 ft
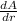 = 2(π × 5) ft²/ft
= 2(π × 5) ft²/ft
or
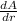 = 10π ft²/ft
= 10π ft²/ft
3) From Pythagoras theorem
Base² + Perpendicular² = Hypotenuse²
Thus,
B² + P² = H² .............(1)
here, H = length of the ladder
P is the height of the wall
B is the distance from the wall at bottom
or
B² + P² = 25² ...........(1)
at B = 20 ft
20² + P² = 25²
or
P² = 625 - 400
or
P = √225
or
P = 15 ft
differentiating (1) with respect to time, we get
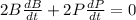
at B = 20 ft,
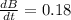 and P = 15 ft
and P = 15 ft
⇒ 2(20)(0.18) +
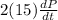 = 0
= 0
or
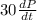 = - 7.2
= - 7.2
or
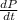 = - 0.24 ft/sec (Here negative sign depicts the ladder slides down)
= - 0.24 ft/sec (Here negative sign depicts the ladder slides down)