Question

A 0.05270.0527 g piece of metal containing an unknown amount of silver is dissolved to form 25.00 mL of solution. To the solution, 35.435.4 mL of 0.02190.0219 M KCl KCl is added, resulting in the complete precipitation of the silver ash AgCl AgCl . The excess Cl−Cl− added to the solution is then back titrated with a standard 0.02190.0219 M AgNO3 AgNO3 solution. A total of 14.3314.33 mL of the standard NaNO3 AgNO3 solution is required to reach the silver chromate end point in the Mohr method. Calculate the percent silver in the piece of metal.

Answer 1

93.30%

Step-by-step explanation:

The equilibrium that takes place is:

• Ag⁺ + Cl⁻ ↔ AgCl(s)

First, let's calculate the total moles of Cl⁻ added to the sample:

• 35.4 mL * 0.0219 M = 0.775 mmol Cl⁻

An unknown amount of this moles reacted with the sample, while the excess was back titrated with a solution containing Ag⁺:

• 14.33 mL * 0.0219 M *
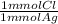  `(1mmolCl)/(1mmolAg)` = 0.314 mmol Cl⁻

Thus, the moles of Cl⁻ that reacted with the sample are:

• 0.775 - 0.314 = 0.461 mmol Cl⁻

Then in the 0.0527 g sample there are 0.461 * 10⁻³ mol Ag, we calculate the mass of Ag in the sample:

• 0.461 * 10⁻³ mol Ag * 107.87 g/mol = 0.0497 g Ag

Finally we calculate the percent silver:

• 0.0497 g / 0.0527 g * 100% = 93.30%