Question

A bottling company uses two inputs to produce bottles of the soft drink​ Sludge: bottling machines​ (K) and workers​ (L). The isoquants have the usual smooth shape. The machines cost​ $1,000 per day to run​ (r), and the workers earn​ $200 per day​ (w). At the current level of​ production, the marginal product of machines ​(MP Subscript Upper K​) is an additional 316 bottles per​ day, and the marginal product of labor ​(MP Subscript Upper L​) is 39 more bottles per day. Is this firm producing at minimum​ cost? If it is minimizing​ cost, explain why. If it is not minimizing​ cost, explain how the firm should change the ratio of inputs it uses to lower its cost.

Answer 1

No.

Step-by-step explanation:

In order to minimizing the cost for a given level of output, the firm should equate the weighted marginal product of capital with the weighted marginal product of labor.

`(MP_(K) )/(r)= (MP_(L) )/(w)`

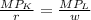
Put the value in the above equation, we get

`(316)/(1,000)= (39)/(200)`

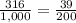
0.316 > 0.195

Now,
`(MP_(K) )/(r)>(MP_(L) )/(w)`, so the firm is not minimizing its cost in producing the bottles of the soft drink​ Sludge.

Hence, in order to minimize cost the firm should substitute labor with more of capital, so that MP 'K' falls and become equal to MP 'L'.