Question

The students in Mr. Wilson's Physics class are making golf ball catapults. The

flight of group A's ball is modeled by the equation y = -0.014x^2 + 0.68x, where x is the ball's
distance from the catapult. The units are in feet.​

a. How far did the ball fly?

b. How high above the ground did the ball fly?

c. What is a reasonable domain and range for this function?

Answer 1

Part a) About 48.6 feet

Part b) About 8.3 feet

Part c) The domain is
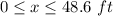`0 \leq x \leq 48.6\ ft` and the range is
`0 \leq y \leq 8.3\ ft`

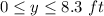
Explanation:

we have

`y=-0.014x^(2) +0.68x`

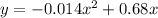
This is a vertical parabola open downward (the leading coefficient is negative)

The vertex represent a maximum

where

x is the ball's distance from the catapult in feet

y is the flight of the balls in feet

Part a) How far did the ball fly?

Find the x-intercepts or the roots of the quadratic equation

Remember that

The x-intercept is the value of x when the value of y is equal to zero

The formula to solve a quadratic equation of the form

`ax^(2) +bx+c=0`

is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}} {2a}`

in this problem we have

`-0.014x^(2) +0.68x=0`

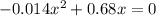
so

`a=-0.014\\b=0.68\\c=0`

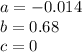
substitute in the formula

`x=\frac{-0.68(+/-)\sqrt{0.68^(2)-4(-0.014)(0)}} {2(-0.014)}`

`x=\frac{-0.68(+/-)0.68} {(-0.028)}`

`x=\frac{-0.68(+)0.68} {(-0.028)}=0`

`x=\frac{-0.68(-)0.68} {(-0.028)}=48.6\ ft`

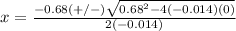
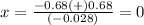
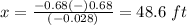
therefore

The ball flew about 48.6 feet

Part b) How high above the ground did the ball fly?

Find the maximum (vertex)

`y=-0.014x^(2) +0.68x`

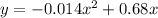
Find out the derivative and equate to zero

`0=-0.028x +0.68`

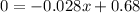
Solve for x

`0.028x=0.68`

`x=24.3`

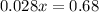
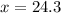
Alternative method

To determine the x-coordinate of the vertex, find out the midpoint between the x-intercepts

`x=(0+48.6)/2=24.3\ ft`

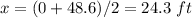
To determine the y-coordinate of the vertex substitute the value of x in the quadratic equation and solve for y

`y=-0.014(24.3)^(2) +0.68(24.3)`

`y=8.3\ ft`

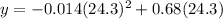
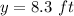
the vertex is the point (24.3,8.3)

therefore

The ball flew above the ground about 8.3 feet

Part c) What is a reasonable domain and range for this function?

we know that

A reasonable domain is the distance between the two x-intercepts

so

`0 \leq x \leq 48.6\ ft`

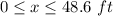
All real numbers greater than or equal to 0 feet and less than or equal to 48.6 feet

A reasonable range is all real numbers greater than or equal to zero and less than or equal to the y-coordinate of the vertex

so

we have the interval -----> [0,8.3]

`0 \leq y \leq 8.3\ ft`

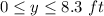
All real numbers greater than or equal to 0 feet and less than or equal to 8.3 feet