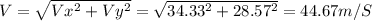Question

A ball is thrown horizontally from the top of a 60.0-m building and lands 100.0 m from the base of thebuilding. Ignore air resistance. (a) How long is the ball in the air? (b) What must havebeen the initialhorizontal component of the velocity? (c) What is the vertical component of the velocity just before the ballhits the ground? (d) What is the velocity (including both the horizontal and vertical components) of the balljust before it hitsthe ground?

Answer 1

a)3.5s

b)28.57m/S

c)34.33m/S

d)44.66m/S

Step-by-step explanation:

Hello!

we will solve this exercise numeral by numeral

a) to find the time the ball takes in the air we must consider that vertically the ball experiences a movement with constant acceleration whose value is gravity (9.81m / S ^ 2), that the initial vertical velocity is zero, we use the following equation for a body that moves with constant acceleration

`Y= VoT+0.5gt^(2)`

where

Vo = Initial speed =0

T = time

g=gravity=9.81m/s^2

y = height=60m

solving for time

`Y=0.5gt^2\\t=\sqrt{(Y)/(0.5g) } \\t=(60)/(0.5(9.81)) \\`

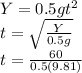
T=3.5s

b)The horizontal speed remains constant since there is no horizontal acceleration. with the value of the distance traveled (100m) and the time that lasts in the air (3.5s) we estimate the horizontal speed

`V=(x)/(t) =(100)/(3.5)=28.57m/s`

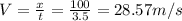
c)

to find the final vertical velocity we use the equations for motion with constant velocity as follows

Vf=Vo+g.t

Vf=0+(9.81 )(3.5)=34.335m/S

d)Finally, to find the resulting velocity, we add the horizontal and vertical velocities vectorially, this is achieved by finding the square root of the sum of its squares

`V=√(Vx^2+Vy^2) =√(34.33^2+28.57^2) =44.67m/S`