Answer:
D.
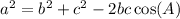
Explanation:
Given any triangle ABC with corresponding side lengths a, b, and c, the law of cosines states the relation between the three sides of triangle and its angles. and they are as follows:
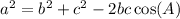
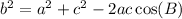
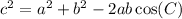
The side opposite angle A is termed as
 , the side opposite angle B is termed as
, the side opposite angle B is termed as
 and the side opposite angle C is termed as
and the side opposite angle C is termed as
 .
.
So, a side of triangle can be obtained using the other two sides and the included angle between the other two sides.
Cosine rule, thus, help in determining the sides of any triangle.
On checking the options, option D matches with the definition of the cosine rule.