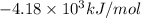Answer :
The specific heat of calorimeter is
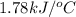
The energy of combustion per mole of vanillin is
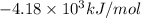
Explanation :
Part 1 :
First we have to calculate the energy released for 0.1625 g of benzoic acid.
Energy released = Energy released × Mass of benzoic acid
Energy released = (26.42 kJ/g) × (0.1625g)
Energy released = -4.293 kJ
Now we have to calculate the specific heat of calorimeter.
Heat released by the reaction = Heat absorbed by the calorimeter
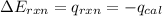
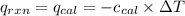
where,
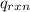 = heat released by the reaction = -4.293 kJ
= heat released by the reaction = -4.293 kJ
 = heat absorbed by the calorimeter
= heat absorbed by the calorimeter
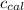 = specific heat of calorimeter = ?
= specific heat of calorimeter = ?
 = change in temperature =
= change in temperature =

Now put all the given values in the above formula, we get:
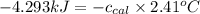
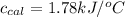
Thus, the specific heat of calorimeter is
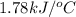
Part 2 :
First we have to calculate the energy released by the reaction.
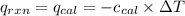
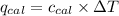
where,
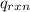 = heat released by the reaction = ?
= heat released by the reaction = ?
 = heat absorbed by the calorimeter
= heat absorbed by the calorimeter
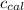 = specific heat of calorimeter =
= specific heat of calorimeter =
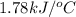
 = change in temperature =
= change in temperature =
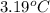
Now put all the given values in the above formula, we get:
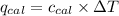
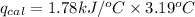
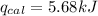
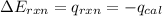

Now we have to calculate the energy of combustion per mole of vanillin.
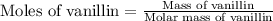
Molar mass of vanillin = 152.15 g/mole
Mass of vanillin = 0.2070 g
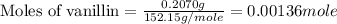
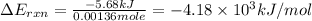
Thus, the energy of combustion per mole of vanillin is