Question

23% of college students say they use credit cards because of the rewards program. You randomly select 10 college students and ask each to name the reason he or she uses credit cards. Find the probability that the number of college students who say they use credit cards because of the rewards program is (a) exactly two, (b) more than two, and (c) between two and five inclusive. If convenient use technology to find the probabilities. P(2) = (Round to the nearest thousandth as needed.) P(x > 2) = (Round to the nearest thousandth as needed.) P(2 x 5)= (Round to the nearest thousandth as needed.)

Answer 1

a) There is a 29.42% probability that the number of college students who say they use credit cards because of the rewards program is exactly two.

b) There is a 41.37% probability that the number of college students who say they use credit cards because of the rewards program is more than two.

c) There is a 69.49% probability that the number of college students who say they use credit cards because of the rewards program is between two and five, inclusive.

Explanation:

There are only two possible outcomes. Either the student use credit cards because of the rewards program, or they use for other reason. So, we can solve this exercise using the binomial probability distribution.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).\pi^(x).(1-\pi)^(n-x)`

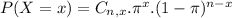
In which
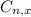`C_(n,x)` is the number of different combinatios of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

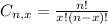
And
`\pi` is the probability of X happening.

In this problem, we have that:

10 students are randomly selected, so
`n = 10`.

23% of college students say they use credit cards because of the rewards program. This means that
`\pi = 0.23`

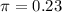
(a) exactly two

This is P(X = 2).

`P(X = x) = C_(n,x).\pi^(x).(1-\pi)^(n-x)`

`P(X = 2) = C_(10,2).(0.23)^(2).(0.77)^(8) = 0.2942`

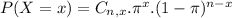
There is a 29.42% probability that the number of college students who say they use credit cards because of the rewards program is exactly two.

(b) more than​ two

This is
`P(X > 2)`.

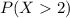Either a value is larger than two, or it is smaller of equal. The sum of the decimal probabilities of these events must be 1. So:

`P(X \leq 2) + P(X > 2) = 1`

`P(X > 2) = 1 - P(X \leq 2)`

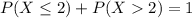
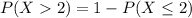
In which

`P(X \leq 2) = P(X = 0) + P(X = 1) + P(X = 2)`

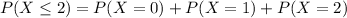
So

`P(X = x) = C_(n,x).\pi^(x).(1-\pi)^(n-x)`

`P(X = 0) = C_(10,0).(0.23)^(0).(0.77)^(10) = 0.0733`

`P(X = 1) = C_(10,1).(0.23)^(1).(0.77)^(9) = 0.2188`

`P(X = 2) = C_(10,2).(0.23)^(2).(0.77)^(8) = 0.2942`

`P(X \leq 2) = P(X = 0) + P(X = 1) + P(X = 2) = 0.0733 + 0.2188 + 0.2942 = 0.5863`

`P(X > 2) = 1 - P(X \leq 2) = 1 - 0.5863 = 0.4137`

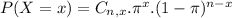
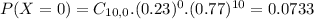
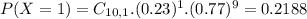
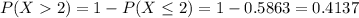
There is a 41.37% probability that the number of college students who say they use credit cards because of the rewards program is more than two.

(c) between two and five inclusive.

This is

`P = P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5)`

`P(X = x) = C_(n,x).\pi^(x).(1-\pi)^(n-x)`

`P(X = 2) = C_(10,2).(0.23)^(2).(0.77)^(8) = 0.2942`

`P(X = 3) = C_(10,3).(0.23)^(3).(0.77)^(7) = 0.2343`

`P(X = 4) = C_(10,4).(0.23)^(4).(0.77)^(6) = 0.1225`

`P(X = 5) = C_(10,3).(0.23)^(5).(0.77)^(5) = 0.0439`

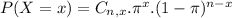
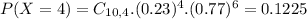
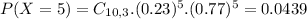
So

`P = P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) = 0.2942 + 0.2343 + 0.1225 + 0.0439 = 0.6949`

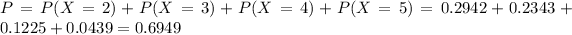
There is a 69.49% probability that the number of college students who say they use credit cards because of the rewards program is between two and five, inclusive.