Question

Water whose temperature is at 100∘C is left to cool in a room where the temperature is 60∘C. After 3 minutes, the water temperature is 90∘. If the water temperature T is a function of time t given by T = 60 + 40 e k t T=60+40ekt, find the time for the water temperature to reach 65∘C. Round to the nearest hundredth of a minute.

Answer 1

21.68 minutes ≈ 21.7 minutes

Explanation:

Given:

`T=60+40e^(kt)`

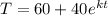
Initial temperature

T = 100°C

Final temperature = 60°C

Temperature after (t = 3 minutes) = 90°C

Now,

using the given equation

`T=60+40e^(kt)`

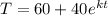
at T = 90°C and t = 3 minutes

`90=60+40e^(k(3))`

`30=40e^(3k)`

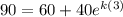
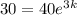
or

`e^(3k)=(3)/(4)`

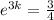
taking the natural log both sides, we get

3k =
`\ln((3)/(4))`

or

3k = -0.2876

or

k = -0.09589

Therefore,

substituting k in 1 for time at temperature, T = 65°C

`65=60+40e^(( -0.09589)t)`

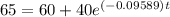
or

`5=40e^(( -0.09589)t)`

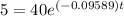
or

`e^(( -0.09589)t)=(5)/(40)`

or

`e^(( -0.09589)t)=0.125`

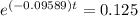
taking the natural log both the sides, we get

( -0.09589)t = ln(0.125)

or

( -0.09589)t = -2.0794

or

t = 21.68 minutes ≈ 21.7 minutes