Answer:
The angular speed of the neutron star is 3130.5 rad/s.
Step-by-step explanation:
Given that,
Initial radius
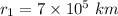
Final radius
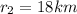
Density of a neutron
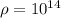
Equal masses of two stars
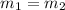
Suppose, If the original star rotated once in 35 days, find the angular speed of the neutron star
Time period of original star T = 35 days = 3024000 s
We need to calculate the initial angular speed of original star
Using formula of angular star
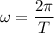
Put the value into the formula
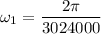
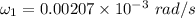
Let the initial moment of inertia of the star is
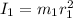
Final moment of inertia of the star is
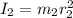
From the conservation of angular momentum
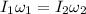
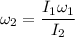
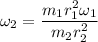
Put the value into the formula
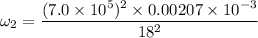

Hence, The angular speed of the neutron star is 3130.5 rad/s.