Question

The life in hours of a 75-watt light bulb is known to be approximately normally distributed, with standard deviation of 25 hours. A random sample of 62 light bulbs has a mean life of 1014 hours. Construct a 98% confidence interval around the true population mean life of the light bulb.

Answer 1

385

Explanation:

We have to find the Sample size through the formula of Margin Error.

The formula is,

`ME = z * (\sigma)/(√(n))`

We have all the values,

ME = 2.5 hours

`\sigma = 25`

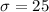
cl = 98% that is in Z-table equal to 2.32

Replacing,

`2.5= 2.32 * (25)/(√(n))`

clearing n,

`n= (1.96*(25)/(2.5))^2`

`n= 384.16`

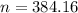
So the least sample size is at least of 385.