Answer:
b)
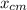 = 4.88 cm , c)
= 4.88 cm , c)
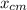 ’= 1/M (m₁ d₁ + m₃ d₃) and d)
’= 1/M (m₁ d₁ + m₃ d₃) and d)
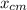 ’= 1.88 cm
’= 1.88 cm
Step-by-step explanation:
The definition of mass center is
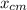 = 1/M ∑ xi mi
= 1/M ∑ xi mi
Where mi, xi are the mass and distance from an origin for each mass and M is the total mass of the object.
Part b
Apply this equation to our case.
Body 1
They give us the mass (m₁ = 24 g) and the distance (d₁ = 1.1 cm) from the origin at the far left
Body 2
They give us the mass (m₂ = 12.g) and the distance relative to the distance of the body 1, let's look for the distance from the left end (origin)
D₂ = d₁ + d₂
D₂ = 1.1 + 1.9
D₂ = 3.0 cm
Body 3
Give the mass (m₃ = 56 g) and the position relative to body 2, let's find the distance relative to the origin
D₃ = D₂ + d₂
D₃ = 3.0 + 3.9
D₃ = 6.9 cm
With this data we substitute and calculate the center of mass
M = m₁ + m₂ + m₃
M = 24 + 12 + 56
M = 92 g
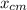 = 1/92 (1.1 24 + 3.0 12 + 6.9 56)
= 1/92 (1.1 24 + 3.0 12 + 6.9 56)
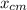 = 1/92 (448.8)
= 1/92 (448.8)
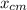 = 4,878 cm
= 4,878 cm
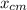 = 4.88 cm
= 4.88 cm
This distance is from the left end of the bar
Par c)
In this case we are asked for the same calculation, but the reference system is in the center marble, we have to rewrite the distance with the reference system in this marble.
Body 1
It is at d1 = -1.9 cm
It is negative for being on the left and the value is the relative distance of 1 to 2
Body 2
d2 = 0 cm
The reference system for her
Body 3
d3 = 3.9 cm
Positive because that is to the left of the reference system and is the relative distance between 2 and 3
Let's write the new center of mass (xcm')
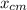 ’= 1/M (m₁ d₁ + m₂ d₂ + m₃ d₃)
’= 1/M (m₁ d₁ + m₂ d₂ + m₃ d₃)
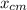 ’= 1/M (m₁ d₁ + m₃ d₃)
’= 1/M (m₁ d₁ + m₃ d₃)
Part d) Let's calculate the value of the center of mass
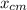 ’= 1/92 ((24 (-1.9) +56 3.9)
’= 1/92 ((24 (-1.9) +56 3.9)
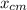 ’= 1/92 (172.8)
’= 1/92 (172.8)
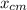 ’= 1.88 cm
’= 1.88 cm
This distance is to the right of the central marble