Question

A new​ phone-answering system installed by a certain utility company is capable of handling twelve calls every 5 minutes. Prior to installing the new​ system, company analysts determined that the incoming calls to the system are Poisson distributed with a mean equal to six every 5 minutes. If the analysts are correct about this incoming call​ distribution, what is the probability that in a 5​-minute period more calls will arrive than the system can​ handle? Based on this​ probability, comment on the adequacy of the new answering system.

Answer 1

A. P(x>12 in 5 minutes)=0.0201

Explanation:

Because we are working with a Poisson Distribution of probability, we need to get all the data needed. In a Poisson distribution is needed a constant called λ that symbolizes the mean data (6 calls) per unit of time (5 minutes), for this distribution λ=6/5.

Poisson probabilities work like this:

`P(x=y\ 'in\ z\ unit\ of\ time')= (e^(-z\lambda)(z\lambda)^(y))/(y!)`

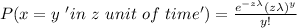
Remember y has to be an integer and the units of z must be the same unit of time used in λ. Now we are ready to solve this problem

A. The question is asking for the probability that in 5 minutes appear more calls than the phone-answering machine could answer (i.e P(x>12 in 5 minutes)). Because there are infinite numbers greater than 12, we are using this property of probabilities that´ll help us simplify the problem:

P(x>12 in 5 minutes)= 1 - P(x≤12 in 5 minutes)

Now we can use the following:

`P(x\geq12\ in\ 5\ minutes)=P(x=0\ in\ 5\ min)+P(x=1\ in\ 5\ min)+...P(x=12\ in\ 5\ min)`

`P(x\geq12\ in\ 5\ minutes)=\sum_(n=0)^(\infty)P(x=n\ in\ 5\min)`

`P(x\geq12\ in\ 5\ minutes)=\sum_(n=0)^(\infty)(e^(-6)6^(n))/(n!)`

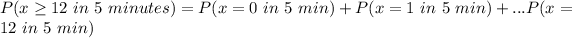
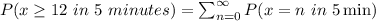
And you can find P(x=n in 5 minutes) for every n using a calculator or a computer, and finally add them to get

P(x≤12 in 5 minutes)= 0.9799

P(x>12 in 5 minutes)= 1-0.9799

This will be our answer

P(x>12 in 5 minutes)= 0.0201