Question

6. Prove that for an integer n, n2 - n is divisible by 2. 7. Prove A SAUB, for all sets A,B

Answer 1

1. We will prove by induction over n, that for an integer n,
`n^2-n` is divisible by 2.

For n= 1,
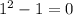`1^2-1=0` and
`(0)/(2)=0`. Then for n=1 the property is satisfied.

Suppose as induction hypothesis that for an integer n,
`n^2-n` is divisible by 2, that is,
`(n^2-n)/(2)=b, \text{ for some integer b}`.

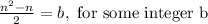Let's see with n+1.

`(n+1)^2-(n+1)=n^2+2n+1-n-1=n^2-n+2n+2`

But,

`(n^2-n+2n+2)/(2)=(n^2-n)/(2)+(2(n+1))/(2)`,

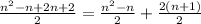by induction hypothesis

`(n^2-n)/(2)+(2(n+1))/(2)=b+(n+1)\in\mathbb{Z}`

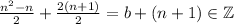
This shows that for n+1 the property is satisfied, then we can conclude that that for an integer n,
`n^2-n` is divisible by 2.

2. Let
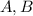`A, B` sets. By definition,

`A\cup B=\{x: x\in A \text{ or } x\in B\}`

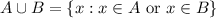
Then, each element of A is in
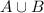`A\cup B`, that is,
`A\subset A\cup B`.