Answer and explanation:
Given : A rectangular frame of uniform depth for a shadow box is to be made from a 36-in. piece of wood.
To find :
a) Write a function to represent the display area in terms of x.
The perimeter of the box is 36 inches.
Let x and y be the length and width of the box.
So,



 ....(1)
....(1)
The area of the box is

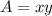
Substitute y from (1),



The function in terms of x,

b. What dimensions should be used to maximize the display area?
As A is a quadratic function with a negative leading coefficient.
The vertex is the maximum point on the function.
So, the x-coordinate of the vertex is the value of x that will maximize the area.
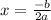
Here, a=-1 and b=18

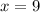
Substitute in (1),

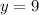
The dimension 9 in. by 9 in. should be used maximize the display area.
c) What is the maximum area?
Substitute the value of x in the area,




The maximum area is 81 square inches.