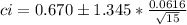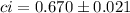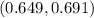Question

A chemist examines "15 sedimentary samples for nitrate concentration. The mean nitrate concentration for the sample data is 0.670 cc/cubic meter with a standard deviation of 0.0616." Determine the 80% confidence interval for the population mean nitrate concentration. Assume the population is approximately normal.

Answer 1

(0.649,0.691)

Explanation:

Basically that is a problem about confidence Interval for a Popuplation Mean.

The formula for confidence interval is given by,

`ci= \bar{x} \pm t*(s)/(√(n))`

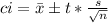
Degree of Freedom,

`DF = 15-1 = 14`

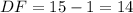
The T-Table say that for 80% ci and DF = 14 the value of t must be 1.345.

`ci = 0.670 \pm 1.345*(0.0616)/(√(15))`

`ci = 0.670 \pm 0.021`

`(0.649,0.691)`