Question

Sammy is playing a board game. He rolls two number cubes, each numbered 1-6. If he rolls a sum of 3 he wins S60 dollars, otherwise he loses

$5 dollars. How much does Sammy expect to win or lose on average per roll.

Answer 1

Sammy is expected to lose $1.39 on average per roll

Explanation:

Since Sammy is rolling two six-sided cubes, the number of possible outcomes is given by:

6 x 6 =36

Out of those 36 outcomes, only two would result in a sum of 3, rolling a 1 and 2 or a 2 and a 1. Therefore, the probability of winning (P(W)) and the probability of losing (P(L)) are:

`P(W) = (2)/(36)= (1)/(18)\\P(L) = 1- (1)/(18)= (17)/(18)`

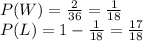
The expected value is defined as the sum of the product of the likelihood of each event by its payout:

`EV = P(W)*\$ W + P(L)*\$ L\\EV = (1)/(18)*60 - (17)/(18)*5\\EV =- \$1.39`

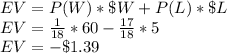
Sammy is expected to lose $1.39 on average per roll.