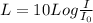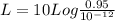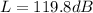Answer:
Part a)
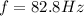
Part b)

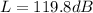
Step-by-step explanation:
Path difference of two sounds reaching at the position of Tom is given as
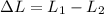
here we know that
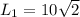
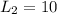
now we have
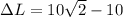
so we know that path difference must be equal to wavelength for maximum intensity of sound
so we have
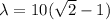
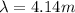
now frequency of sound is given as
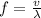

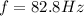
Part b)
Intensity of source at position of Tom is given as
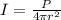
so we have
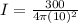
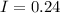
now due to constructive interference the maximum intensity is given as
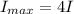

now sound level is given as