Answer:
- 0.100
Explanation:
Length of the ladder, H = 6 m
Distance at the bottom from the wall, B = 1.3 m
Let the distance of top of the ladder from the bottom at the wall is P
Thus,
from Pythagoras theorem,
B² + P² = H² .
or
B² + P² = 6² ..............(1) [Since length of the ladder remains constant]
at B = 1.3 m
1.3² + P² = 6²
or
P² = 36 - 1.69
or
P² = 34.31
or
P = 5.857
Now,
differentiating (1)
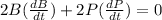
at t = 2 seconds
change in B = 0.3 × 2= 0.6 ft
Thus,
at 2 seconds
B = 1.3 + 0.6 = 1.9 m
therefore,
1.9² + P² = 6²
or
P = 5.69 m
on substituting the given values,
2(1.9)(0.3) + 2(5.69) ×
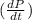 = 0
= 0
or
1.14 + 11.38 ×
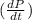 = 0
= 0
or
11.38 ×
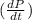 = - 1.14
= - 1.14
or
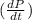 = - 0.100
= - 0.100
here, negative sign means that the velocity is in downward direction as upward is positive