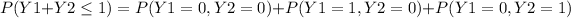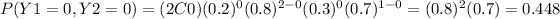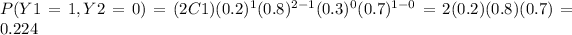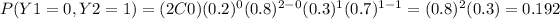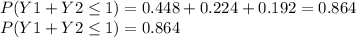Question

A supermarket has two customers waiting to pay for their purchases at counter I and one customer waiting to pay at counter II. Let Y1 and Y2 denote the numbers of customers who spend more than $50 on groceries at the respective counters. Suppose that Y1 and Y2 are independent binomial random variables, with the probability that a customer at counter I will spend more than $50 equal to .2 and the probability that a customer at counter II will spend more than $50 equal to .3. Find the a joint probability distribution for Y1 and Y2. b probability that not more than one of the three customers will spend more than $50.

Answer 1

b. 0.864

Explanation:

Let's start defining the random variables.

Y1 : ''Number of customers who spend more than $50 on groceries at counter 1''

Y2 : ''Number of customers who spend more than $50 on groceries at counter 2''

If X is a binomial random variable, the probability function for X is :

`P(X=x)=(nCx)p^(x)(1-p)^(n-x)`

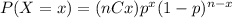
Where P(X=x) is the probability of the random variable X to assume the value x

nCx is the combinatorial number define as :

`nCx=(n!)/(x!(n-x)!)`

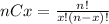
n is the number of independent Bernoulli experiments taking place

And p is the success probability.

In counter I :

Y1 ~ Bi (n,p)

Y1 ~ Bi(2,0.2)

`P(Y1=y1)=(2Cy1)(0.2)^(y1)(0.8)^(2-y1)`

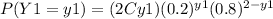
With y1 ∈ {0,1,2}

And P( Y1 = y1 ) = 0 with y1 ∉ {0,1,2}

In counter II :

Y2 ~ Bi (n,p)

Y2 ~ Bi (1,0.3)

`P(Y2=y2)=(1Cy2)(0.3)^(y2)(0.7)^(1-y2)`

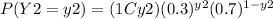
With y2 ∈ {0,1}

And P( Y2 = y2 ) = 0 with y2 ∉ {0,1}

(1Cy2) with y2 = 0 and y2 = 1 is equal to 1 so the probability function for Y2 is :

`P(Y2=y2)=(0.3)^(y2)(0.7)^(1-y2)`

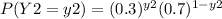
Y1 and Y2 are independent so the joint probability distribution is the product of the Y1 probability function and the Y2 probability function.

`P(Y1=y1,Y2=y2)=P(Y1=y1).P(Y2=y2)`

`P(Y1=y1,Y2=y2)=(2Cy1)(0.2)^(y1)(0.8)^(2-y1)(0.3)^(y2)(0.7)^(1-y2)`

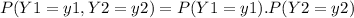
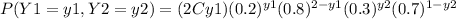
With y1 ∈ {0,1,2} and y2 ∈ {0,1}

P( Y1 = y1 , Y2 = y2) = 0 when y1 ∉ {0,1,2} or y2 ∉ {0,1}

b. Not more than one of three customers will spend more than $50 can mathematically be expressed as :

`Y1 + Y2 \leq 1`

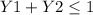
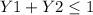`Y1 + Y2\leq 1` when Y1 = 0 and Y2 = 0 , when Y1 = 1 and Y2 = 0 and finally when Y1 = 0 and Y2 = 1

To calculate
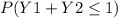`P(Y1+Y2\leq 1)` we must sume all the probabilities that satisfy the equation :

`P(Y1+Y2\leq 1)=P(Y1=0,Y2=0)+P(Y1=1,Y2=0)+P(Y1=0,Y2=1)`

`P(Y1=0,Y2=0)=(2C0)(0.2)^(0)(0.8)^(2-0)(0.3)^(0)(0.7)^(1-0)=(0.8)^(2)(0.7)=0.448`

`P(Y1=1,Y2=0)=(2C1)(0.2)^(1)(0.8)^(2-1)(0.3)^(0)(0.7)^(1-0)=2(0.2)(0.8)(0.7)=0.224`

`P(Y1=0,Y2=1)=(2C0)(0.2)^(0)(0.8)^(2-0)(0.3)^(1)(0.7)^(1-1)=(0.8)^(2)(0.3)=0.192`

`P(Y1+Y2\leq 1)=0.448+0.224+0.192=0.864\\P(Y1+Y2\leq 1)=0.864`