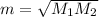Question

A rod of negligible mass is pivoted at a point that is off-center, so that length ?1 is different from length ?2. The figures show two cases in which masses are suspended from the ends of the rod. In each case the unknown mass m is balanced by a known mass M1 or M2 so that the rod remains horizontal. TTL Mi e1 Tn

What is the value of m in terms of the known masses?

1. m = p M1 M2

2. m = M1 M2

3. m = M1 + M2 2

4. m = M1 M2 2

5. m = M1 + M2

Answer 1

`m = √(M_1 M_2)`

Step-by-step explanation:

Two casess are mentioned in the given figure

first case

two mass m and M_1

m is l_1 distance from center and M_1 is l_2 distance from center

second case

two mass m and M_2

m is l_2 distance from center and M_2 is l_1 distance from center

The balance in the 1st case requires
`m l_1 = M_1 l_2.`

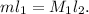
And the balance in second case

`M_2 l_1 = m l_2.`

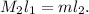
Cancel
`l_1 and l_2`

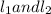
from the above equations.

So
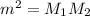`m^2 = M_1 M_2`, i.e.

`m = √(M_1 M_2)`