Question

Long division 12p^5+20p^4+18p^2+45p+25/3p+5

Answer 1

`4p^4+6p+5`

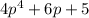
Explanation:

Given

`(12p^5+20p^4+18p^2+45^p+25)/(3p+5)`

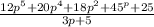
Step 1:

Now Dividing the above Equation our first quotient will be
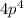`4p^4` and First remainder will be
`18p^2+45p`

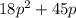
Step 2:

Now Dividing the First remainder
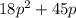`18p^2+45p` with
`3p+5`

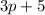
now our second Quotient will be
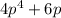`4p^4+6p` and Second remainder will be
`15p+25`

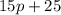
Step 3:

Now Dividing Second remainder
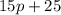`15p+25` with
`3p+5`

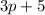
now our third Quotient will be
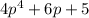`4p^4+6p +5` and Remainder will be 0.

`\therefore` Our Final Answer is
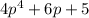`4p^4+6p +5` with remainder 0