Question

A boat moves north at a speed of 2.7 m/s across a river that flows west at a rate of 1.2 m/s What is the boat's speed relative to the riverbank?

Answer 1

The boat speed relative to the riverbank is 2.96 m/s

Step-by-step explanation:

The boat move to the north at 2.7 m/s across the river and the river current is 1.2 m/s to the west, therefore the direction of the boat is perpendicular to the river (90
`90^(o)`).

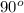The boat speed vb = 2.7 m/s

The current speed vc = 1.2 m/s

The formula to calculate the speed of the boad relative to the riverbanks (Vbc), as follow

vbc =
`\sqrt{vb^(2)+vc^(2)+2*vb*vc*cos 90^(2)  }`

=
`\sqrt{2.7^(2)+1.2^(2) +2* 2.7*1.2*cos 90^(o) }`

since cos 90 = 0, hence

vbc =
`\sqrt{2.7^(2)+1.2^(2) }`

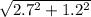
= 2.96 m/s