Question

Please help a 15 points

Rectangle R has varying length l and width w but a constant perimeter of 4 ft.

a. Express the area A as a function of l. What do you know about this function?

b. For what values off and w will the area of Rbe greatest? Give an algebraic
argument. Give a geometric argument.

Answer 1

a. A = l(2 - l)

b. l = 1 foot and w = 1 foot.

Explanation:

With a constant perimeter of 4 feet, a rectangle has variable length l and variable width w.

So, 2(l + w) = 4

⇒ l + w = 2 .........(1)

⇒ w = 2 - l ........(2)

a. Now, area of the rectangle will be A = lw = l(2 - l) ......... (3) {From equation (2)}

b. For A to be maximum, the condition is
`(dA)/(dl) =0`.

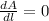Now, from equation (3), differentiating with respect to l, we get

`(dA)/(dl) =2-2l = 0`.

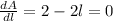⇒ l = 1 feet.

Hence, w = 1 feet.

So, when the length and width of the rectangle are the same and equal to 1 foot, then only the area will be maximum.

That means, when the rectangle becomes a square, then the area will be maximum.