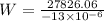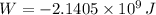Answer:
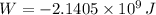
Step-by-step explanation:
Given:
electric field,
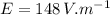
charge,
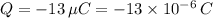
initial position coordinates,
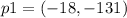
final position coordinates,
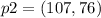
We find the distance through which the charge has been moved:
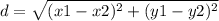
Where we have (x1,y1) & (x2,y2) as the initial and final coordinates of the points.
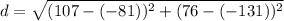
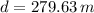
Now we need the angle through which displacement is made with respect to the direction of electric field.
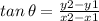
![\theta= tan^(-1)[(76-(-131))/(107-(-81)) ]](https://img.qammunity.org/2020/formulas/physics/college/7r7xhx1spop29ukz4w1fokffp0dfbx7ih1.png)
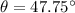
Now from the relation between the change in potential difference:
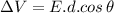
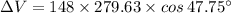
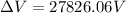
∵The change in voltage is defined as the work done per unit charge.
∴
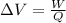
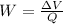
Putting the respective values