Question

The time between telephone calls to a cable television service call center follows an exponential distribution with a mean of 1.2 minutes. a. What is the probability that the time between the next two calls will be 54 seconds or​ less? b. What is the probability that the time between the next two calls will be greater than 118.5 ​seconds?

Answer 1

0.52763 is the probability that the time between the next two calls will be 54 seconds or​ less.

0.19285 is the probability that the time between the next two calls will be greater than 118.5 ​seconds.

Explanation:

We are given the following information in the question:

The time between telephone calls to a cable television service call center follows an exponential distribution with a mean of 1.2 minutes.

The distribution function can be written as:

`f(x) = \lambda e^(-\lambda x)\\\text{where lambda is the parameter}\\\\\text{Mean} = \mu = \displaystyle(1)/(\lambda)\\\\\Rightarrow 1.2 = (1)/(\lambda)\\\\\lambda = 0.84 \\f(x) = 0.84 e^(0.84 x)`

The probability for exponential distribution is given as:

`P( x \leq a) = 1 - e^{(-a)/(\mu)}\\\\P(a \leq x \leq b) = e^{(-a)/(\mu) -(-b)/(\mu)}`

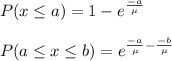
a) P( time between the next two calls will be 54 seconds or​ less)

`P( x \leq 0.9)\\= 1 - e^{((-54)/(60))/(1.2)} = 0.52763`

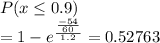
0.52763 is the probability that the time between the next two calls will be 54 seconds or​ less.

b) P(time between the next two calls will be greater than 118.5 ​seconds)

`p( x > (118.5)/(60)) = P(x > 1.975)\\\\ = 1 - P(x \leq 1.975) \\\\= 1 -1+ e^{(-1.975)/(1.2)}\\\\= 0.19285`

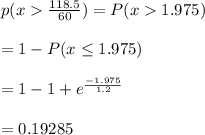
0.19285 is the probability that the time between the next two calls will be greater than 118.5 ​seconds.