Question

Singly charged uranium-238 ions are accelerated through a potential difference of 2.26 kV and enter a uniform magnetic field of magnitude 1.98 T directed perpendicular to their velocities. (a) Determine the radius of their circular path. (Give your answer to three significant figures.) ............ cm (b) Repeat this calculation for uranium-235 ions. (Give your answer to three significant figures.) ............ cm (c) How does the ratio of these path radii depend on the accelerating voltage? (d) How does the ratio of these path radii depend on the magnitude of the magnetic field?

Answer 1

Step-by-step explanation:

It is given that,

Mass of singly charged uranium 238 is,
`m=3.95* 10^(-25)\ kg`

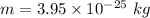
Potential difference,
`V=2.26\ kV=2.26* 10^3\ V`

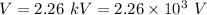
Magnetic field, B = 1.98 T

(a) Let r is the radius of their circular path. It is given by :

`r=(1)/(B)\sqrt{(2mV)/(q)}`

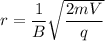
q is the charge on electron

`r=(1)/(1.98)\sqrt{(2* 3.95* 10^(-25)* 2.26* 10^3)/(1.6* 10^(-19))}`

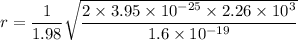
r = 0.05335 meters

(b) Mass of singly charged uranium 235 is,
`m=3.9* 10^(-25)\ kg`

`r=(1)/(B)\sqrt{(2mV)/(q)}`

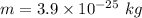
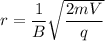
q is the charge on electron

`r=(1)/(1.98)\sqrt{(2* 3.9* 10^(-25)* 2.26* 10^3)/(1.6* 10^(-19))}`

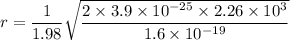
r = 0.053012 meters

(c) The radius of the acceleration voltage depends on the radius of path. Here, the voltage is same but for heavier ion the radius is more as compared to the lighter ion. The ratio is nor dependent on the accelerating voltage

(d) The ratio of these path radii do not depend on the magnitude of the magnetic field.

Hence, this is the required solution.