Question

A circle fits in a square with sides of 12 inches. What is the approximate area of the shaded region between the square and the

circle? (Use 3.14 for and round to the nearest whole number.)
12 inches
12 inches
31 in 2
69 in 2
106 in 2
125 in.

Answer 1

31in(2) is the answer

Answer 2

31 in²

Explanation:

If your problem is like the one attached then you can solve this by first determining the area of the circle and the square:

The formula for the area of a square is:

A = s²

Where:

A = Area of the square

s = side of a square

A = s²

A = 12in²

A = 144in²

The area of a circle on the other hand can be computed with the formula:

A = πr²

Where:

A = area of the circle

π = 3.14

r = radius

Because one side of the square is 12 inches and the circle fits into it perfectly, then the diameter (the distance between two points of the circle that crosses the center of the circle) is 12 inches as well. The radius is half of the diameter (The distance between a point on the circle from the center.)

`r = (d)/(2) = (12in)/(2) = 6 in`

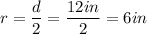
Now we plug it in:

`A = \pi r^2\\\\A = (3.14)(6in)^2\\\\A = (3.14)(36in^2)\\\\A = 113.04 in^2`

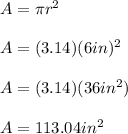
So now that you have the area of both, you just subtract the area of the circle from the area of the square.

144 in² - 113.04 in² = 30.96 in² ≅ 31in²