Question

If exactly 220 people sign up for a charter flight, Leisure World Travel Agency charges $282/person. However, if more than 220 people sign up for the flight (assume this is the case), then every fare is reduced by $1 times the number of passengers above 220. Determine how many passengers will result in a maximum revenue for the travel agency. Hint: Let x denote the number of passengers above 220. Show that the revenue function R is given by R(x)

Answer 1

251 passengers will result in a maximum revenue.

Explanation:

The price per ticket of the first 220 passengers is given by:

`220*(282-x)`

The price per ticket of the additional x passengers is:

`x(282 - x)`

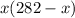
Adding both parts gives us the revenue function R(x):

`R = 220*(282 -x) + x(282-x)`

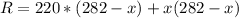
The term (282-x) is present in both parts and can be factored:

`R(x)= (220+x)*(282-x)\\R(x)= -x^2 +62x+ 62,040`

To find how many passengers will result in a maximum revenue, derive the function R(x) and find its zeroes:

`(d)/(dx)R(x)= (d)/(dx) (-x^2 +62x+ 62,040)\\(d)/(dx)R(x)=-2x +62 = 0\\x=(62)/(2)\\x=31`

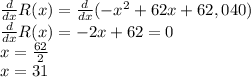
31 passengers above 220 will result in a maximum revenue. Therefore, 251 passengers will result in a maximum revenue.