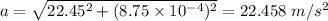Answer:
(a)

(b)
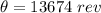
(c)
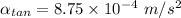
(d)
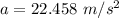
Solution:
As per the question:
Angular velocity,

Time taken by the wheel to stop, t = 2.4 h =
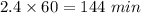
Distance from the axis, R = 38 cm = 0.38 m
Now,
(a) To calculate the constant angular velocity, suing Kinematic eqn for rotational motion:

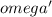 = final angular velocity
= final angular velocity
 = initial angular velocity
= initial angular velocity
 = angular acceleration
= angular acceleration
Now,
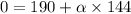

Now,
(b) The no. of revolutions is given by:
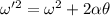
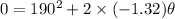
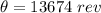
(c) Tangential component does not depend on instantaneous angular velocity but depends on radius and angular acceleration:
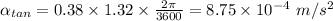
(d) The radial acceleration is given by:
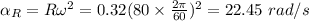
Linear acceleration is given by: