Question

A conjecture and the flowchart proof used to prove the conjecture are shown.

Given: A B C D is a parallelogram. Prove: Angle 1 is supplementary to angle 3. Art: Parallelogram A B C D. Ray D B is drawn and is extended past vertex B. The ray forms an interior angles A D B and D B C and an exterior angle labeled as 3, adjacent to angle D B C. Angle A D B is labeled as 1, and angle D B C is labeled as 2.




Drag an expression or phrase to each box to complete the proof.

Answer 1

my best answer would be 2

Explanation:

Answer 2

∠1 is supplementary to ∠3.

Explanation:

Given information: ABCD is a parallelogram.

Prove: ∠1 is supplementary to ∠3.

Proof:

∠1 = ∠ADB

∠2 = ∠DBC

∠3 = exterior angle adjacent to angle D B C.

Statement Reason

∠2 is supplementary to ∠3 Linear pairs

m∠2+m∠3=180° Definition of supplementary angles

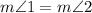`m\angle 1=m\angle 2` Alternative interior angles

m∠1+m∠3=180° Substitute property of equality

∠1 is supplementary to ∠3 Definition of supplementary angles

Hence proved.