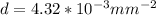Answer:
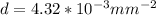
Step-by-step explanation:
We need to find the constant for the particular material given by the yield strenght equation,
That is,
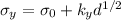
Where
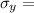 The yield strenght
The yield strenght
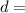 Average grain diameter
Average grain diameter
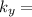 constant for the particular material
constant for the particular material
Our values are,
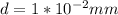
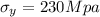
Substituting for
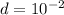 mm and 230Mpa for
mm and 230Mpa for
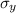 ,
,
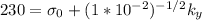
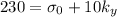 (1)
(1)
Substituting for
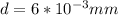 and 275Mpa for
and 275Mpa for
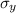 ,
,
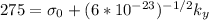
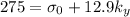 (2)
(2)
Solving the two values (1) and (2) we have,
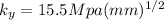
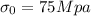
Substituting now for 310Mpa calculate 310Mpa
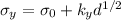
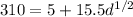
Solving for d,