Question

A group of students is arranging squares into layers to create a project. The first layer has 6 squares. The second layer has 12 squares. Which formula represents an arithmetic explicit formula to determine the number of squares in each layer?

a1 = 6; an = 6 + an − 1, n > 0



a1 = 6; an = 6 ⋅ an − 1, n > 0



a1 = 6; an = 6 ⋅ an + 1, n > 0



a1 = 6; an = 6 + an + 1, n > 0

Answer 1

`a_n=6n`

Explanation:

This is an example of an arithmetic sequence that is that the following term is obtained by adding or substracting a number called difference the formula for this sequence is:

`a_n=a_1+d(n-1)`

In this case your first term is:

`a_1=6`

and your difference is

`d=6`

substituting these values we have that

`a_(n)=6+6(n-1) \\a_n=6+6n-6\\a_n=6n`

Answer 2

Option 1.

Explicit formula :
`a_n=6n`

Recursive formula :
`a_n=a_(n-1)+6`

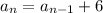
Explanation:

All options represent the recursive formulas.

It is given that the first layer has 6 squares. The second layer has 12 squares.

`a_1=6`

`a_2=12`

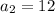
It represents an arithmetic sequence 6, 12, 18, ....

Common difference is

`d=a_2-a_1=12-6`

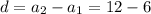
The explicit formula of an AP is

`a_n=a+(n-1)d`

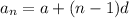
where, a is first term and d is common difference.

Substitute a=6 and d=6 to find the explicit formula for given situation.

`a_n=6+(n-1)6`

`a_n=6+6n-6`

`a_n=6n`

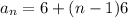
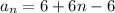
The recursive formula of an AP is

`a_n=a_(n-1)+d`

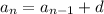
Substitute d=6 to find the recursive formula for given situation.

`a_n=a_(n-1)+6`

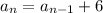
where, n>0.

Therefore, the correct option is 1.