Answer:
Time taken to stop the door is 5 s
Solution:
As per the question:
Angular speed,
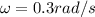
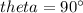
Angular acceleration,

Now,
Using Kinematic eqn for rotational motion:
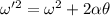
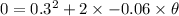
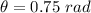
Since, the value of
 <
<
 , thus we will able to stop the door before it closes.
, thus we will able to stop the door before it closes.
Time taken to stop the door, t :


t = 5 s