Answer:
a)
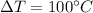
b)
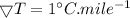
c)

d)

Step-by-step explanation:
Given is the data of variation of temperature with respect to the distance traveled:
Temperature T as a function of distance d:
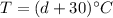 ...................................(1)
...................................(1)
(a)
Total change in temperature from the start till the end of the journey:
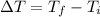 ..............................(2)
..............................(2)
where:
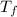 = final temperature
= final temperature
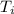 = initial temperature
= initial temperature
∵In the start of the journey d = 0 miles & at the end of the journey d = 100 miles.
So, correspondingly we have the eq. (2) & (1) as:
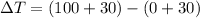
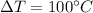
(b)
Now, the average rate of change of the temperature, with respect to distance, from the beginning of the trip to the end of the trip be calculated as:
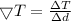 ......................(3)
......................(3)
where:
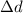 = change in distance
= change in distance
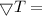 change in temperature with respect to distance
change in temperature with respect to distance
putting the respective values in eq. (3)
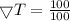
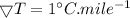
(c)
comparing the given function of the temperature with the general equation of a straight line:
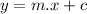
We find that we have the slope of the equation as 1 throughout the journey and therefore the rate of change in temperature with respect to distance remains constant.

(d)
comparing the given function of the temperature with the general equation of a straight line:
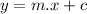
We find that we have the slope of the equation as 1 throughout the journey and therefore the rate of change in temperature with respect to distance remains constant.
