Question

A company produces and sells 5,000 boxes of playing cards each year. Each production run has a fixed cost of $200 and an additional cost of $2 per box of playing cards. To store a box for a full year costs $2. What is the optimal number of boxes of playing cards the company should make during each production run? Do not include units with your answer.

Answer 1

no of box per production is 1000

Step-by-step explanation:

given data

produces and sells = 5,000 boxes

fixed cost = $200

additional cost = $2 per box

full year costs = $2

to find out

optimal number of boxes of playing cards the company should make during each production run

solution

we consider optimal number of box is x

so

yearly storing cost = yearly storage cost per item × average no of item carried

yearly storing cost = 2 ×
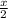`(x)/(2)` = x

and

yearly recording cost = cost during each order × no of order place per year

yearly recording cost = 200 + 2x ×
`(5000)/(x)`

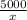
so

total cost = x + ( 200 + 2x ) ×
`(5000)/(x)`

C(x) = x +
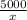
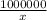`(1000000)/(x)` + 10000

so for minimum cost

C'(x) = 1 +
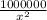`(1000000)/(x^2)` = 0

x = 1000

so no of box per production is 1000