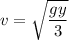Question

An Atwood's machine consists of two different masses, both hanging vertically and connected by an ideal string which passes over a pulley. Let the masses be M1 and M2 and M2 = 2M1. Initially, M1 is held fixed a distance y below M2. Find the speed of the blocks when they are the same elevation (that is, the same horizontal position, by then each block has moved y/2). Use Work and Kinetic Energy.

Please show work. A picture as well would be much appreciated.

Answer 1

`v=\sqrt{(gy)/(3)}`

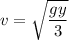
Step-by-step explanation:

Given that

M₂ = 2M₁

Lets take speed of the block is v.

From energy conservation

U₁+KE₁= U₂+ KE₂

M₁ x g x 0 + M₂ x g x y = M₁ x g x y/2 + M₂ x g x y/2 + 1/2 v²( M₁+ M₂ )

2M₂g y = M₁ g y + M₂ g y + v²( M₁+ M₂ )

gy ( 2M₂- M₁ -M₂ ) = v²( M₁+ M₂ )

M₂ = 2M₁

gy ( 4 M₁ - M₁ -2 M₁ ) = v²( M₁+ 2M₁ )

gy M₁ = 3 M₁v²

gy = 3 v²

`v=\sqrt{(gy)/(3)}`