Question

A mixture of carbon dioxide and hydrogen gases is maintained in a 6.68 L flask at a pressure of 2.14 atm and a temperature of 19 °C. If the gas mixture contains 16.8 grams of carbon dioxide, the number of grams of hydrogen in the mixture is how many grams?

I don't need the answer, but if I could just get instructions on how...that'd be great.

Answer 1

The mass of hydrogen gas in the mixture: w₂ = 0.433 g

Step-by-step explanation:

According to the ideal gas equation:

for an ideal gas,
`P.V = n_(total).R.T`

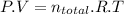
and
`n_(total)= n_(1)+n_(2)`

Here, P: total pressure of the gases = 2.14 atm

V: total volume of the gases = 6.68 L

T: temperature = 19 °C = 19+273.15 = 292.15K (∵ 0°C = 273.15K)

R: gas constant = 0.08206 L·atm·K⁻¹·mol⁻¹

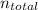`n_(total)`: total number of moles of gases

To calculate the total number of moles of gases:

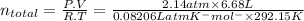`n_(total) = (P.V)/(R.T) = (2.14 atm* 6.68 L)/(0.08206 LatmK^(-)mol^(-)* 292.15K)` = 0.5963 moles

Let, the number of moles of carbon dioxide be n₁ and number of moles of hydrogen be n₂

Given: mass of carbon dioxide: w₁ = 16.8 g, mass of hydrogen: w₂ = ?g

molar mass of carbon dioxide: m₁ = 44.01 g/mol, molar mass of hydrogen: m₂= 2.016 g/mol

Therefore,
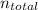`n_(total)`= n_{1}+n_{2} = (w₁ ÷ m₁) + (w₂ ÷ m₂)

⇒ 0.5963 mol = (16.8 g ÷ 44.01 g/mol) + (w₂ ÷ 2.016 g/mol)

⇒ 0.5963 mol = (0.3817mol) + (w₂ ÷ 2.016 g/mol)

⇒ 0.5963 mol - 0.3817mol = (w₂ ÷ 2.016 g/mol)

⇒ 0.2146 mol = (w₂ ÷ 2.016 g/mol)

⇒ w₂ = 0.433 g

Therefore, the mass of hydrogen gas in the mixture: w₂ = 0.433 g