Answer:
See proof below
Explanation:
If we consider 2 PM as hour 0, then 10 minutes later would be hour 1/6 (since 10 minutes equals 1/6 hours).
If V(t) is the speed at hour t, because of the Mean Value Theorem, there exists a point c in [0, 1/6] such that
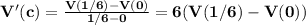
But
V(0) = 30 m/h and V(1/6) = 50 m/h, hence

Since V'(c) is the acceleration at hour c, the proof is complete.