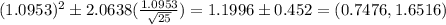Answer:
Confidence interval for the population variance = (0.7476,1.6516)
Explanation:
We are given the following information in the question:
n = 25
Sample mean,
 = 29.530 inches
= 29.530 inches
Alpha, α = 0.05
Sample standard deviation, s = 1.0953 inches
Confidence interval:
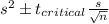
Putting the values, we get,