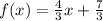What function describes a line with slope 4/3 and passing through the point (2,5) ?

Question

asked Feb 24, 2020 171k views

1 Answer

Pikapops · Answer 1 · 2020-03-01T02:20:51+0000

For this case we have that by definition, the equation of the line of the slope-intersection form is given by:

y = mx + b

Where:

m: It's the slope

b: It is the cut-off point with the y axis

According to the data of the statement we have to:

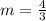
$m = \frac {4} {3}$

Thus, the equation is of the form:

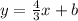
$y = \frac {4} {3} x + b$

We substitute the given point
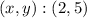(x, y) :( 2,5) and find the cut-off point:

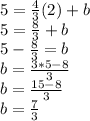
$5 = \frac {4} {3} (2) + b\\5 = \frac {8} {3} + b\\5- \frac {8} {3} = b\\b = \frac {3 * 5-8} {3}\\b = \frac {15-8} {3}\\b = \frac {7} {3}$

Thus, the equation is:
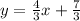
$y = \frac {4} {3} x + \frac {7} {3}$

Finally, we have that the function is of the form
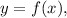y = f (x), where
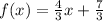
$f (x)=\frac {4} {3} x + \frac {7} {3}$

ANswer:

$f (x) = \frac {4} {3} x + \frac {7} {3}$