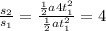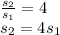Answer:
The correct answer is D. s₂=4s₁
Step-by-step explanation:
The distance of a particle is given by:
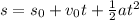
where
s₀ is the initial position when t=0
v₀ is the initial speed when t=0
a is the constant acceleration
t is the time in seconds
Then, the position s₁ is given by:
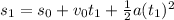
As the particle starts from rest v₀=0 and we consider s₀=0, s₁ will be:
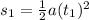
Furthermore, the position s₂ is:
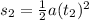
In this case t₁=10 s and t₂=20 s (10 seconds later). In other words t₂=2t₁.
We replace the value of t₂ in the second equation (s₂):
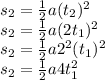
Finally, we divide s₂ by s₁ to get the ratio: