Question

A parallelogram has vertices A(0,4), B(2, 2), C(4,4),

and D(26) Is this parallelogram a square? Explain why


or why not

Answer 1

yes, parallelogram ABCD is a square.

Explanation:

Given information: ABCD is parallelogram with vertices A(0,4), B(2, 2), C(4,4), and D(2,6).

We need to check whether this parallelogram is a square or not.

The opposite side of a parallelogram are parallel and congruent. If the interior angles a parallelogram are right angles then the parallelogram is square.

Formula for slope:

`m=(y_2-y_1)/(x_2-x_1)`

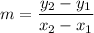
Now, find the slopes of each side.

`m_(AB)=(2-4)/(2-0)=-1`

`m_(BC)=(4-2)/(4-2)=1`

`m_(CD)=(6-4)/(2-4)=-1`

`m_(AD)=(6-4)/(2-0)=1`

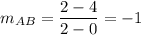
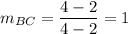
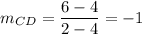
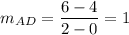
The product of slopes of two perpendicular line is -1.

The product of slopes of any two consecutive sides is -1. It means all interior angles are right angle.

Therefore, the parallelogram ABCD is a square.